tl;dr, I made a program for translating vanilla siteswaps into animations of how a 3-handed person might juggle them. You can play with it here. If you are interested in the source code, it’s available on my github.

Background

Last January, Michael Karas approached me with an idea:

“I’m interested in having a 3 handed juggling simulator created where the hands are labeled L, M, and R. The default throwing sequence would be L, M, R, M. So if all 3 hands are juggling 2 in 1 hand, the siteswap would be ‘84’”

I’m a big fan of Michael’s juggling and I love to geek out about siteswap so I was naturally excited about the project.

Jugglinglab

I wrote a custom juggling animator in javascript for juggle-suggest2, but modifying it to support a third hand would have taken me weeks of work. Instead, I decided it would be easier to write a translator to take vanilla siteswap and output links to the jugglinglab gif server.

To learn more about how jugglinglab handles several jugglers, I reached out to Dominik Braun, author of the amazing Fun with Juggling Lab series. Dominik told me that jugglinglab doesn’t support arbitrary hand orderings but pointed out that I could fake it by translating patterns to sync notation and padding with 0’s where appropriate.

Async to Sync Translation

There’s a pretty easy procedure to take an async pattern and get something analogous but for two sync hands:

First double all the numbers, then add x’s to all the ones that were previously odd. Now slot those numbers into (0,_)(_,0)(0,_)(_,0)…

And finally, if the siteswap length is odd, we’ll need to slot it in twice, that way we cover both sides of the pattern.

If you think about what this procedure does - it makes a lot of sense. The doubling is because sync beats happen half as often. The x’s are because you need to know which hand a ball lands in, and the * is because odd length siteswaps alternate sides.

So, in a 3-handed world, we can do almost the same procedure.

First we double all numbers in the pattern. Then we suffix them with x’s, p’s and xp’s to make them land in the correct hand. Then we slot them into <(_,0)(0,_)(0,0)(0,_)…|(0,0)(0,0)(_,0)(0,0)>.

And if the pattern length isn’t divisible by 4, we slot it in LCM(length, 4) times to make sure we cover all positions in the cycle.

As I was implementing this, I realized that LMRM is a special case, and I might as well handle other hand orders as well. This barely changes the procedure! The only difference is computing which suffix gets applied to which throw, and computing what string to slot into.

Too Much Empty Space

I sent some demo gifs to Michael, and he said they didn’t look how he was expecting. He pointed out how much time hands were spending empty, and then showed me some more demo videos of human jugglers doing these patterns.

These two gifs show how my program was rendering siteswap 35, versus how Michael was imagining it.

Mine:

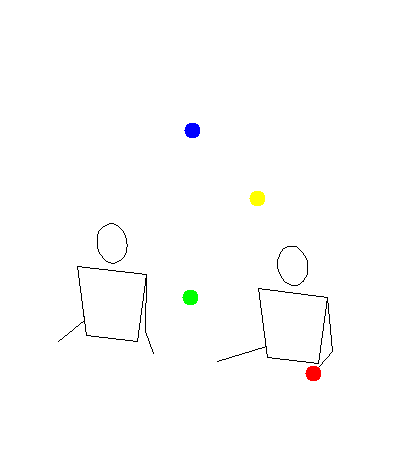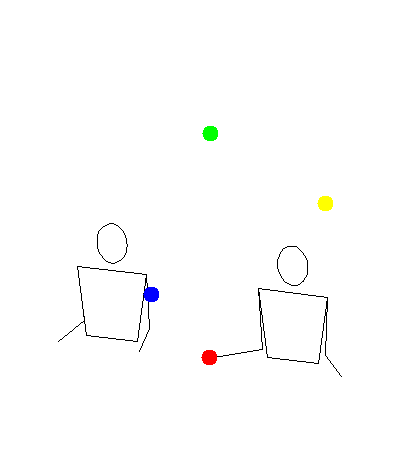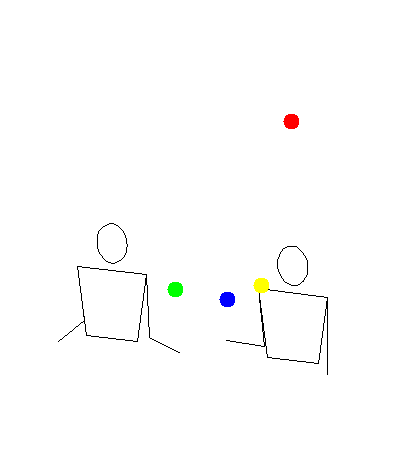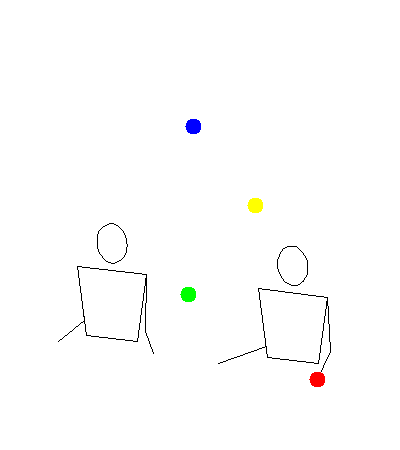
Michael’s:

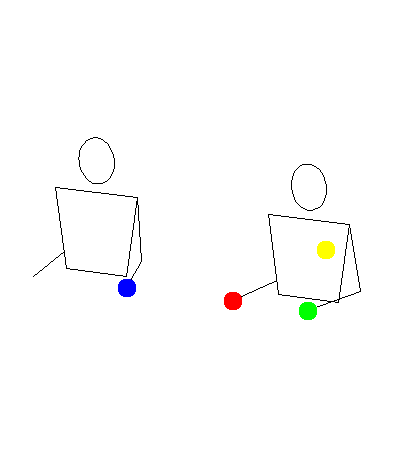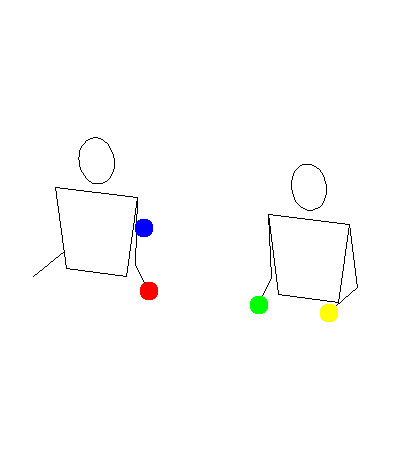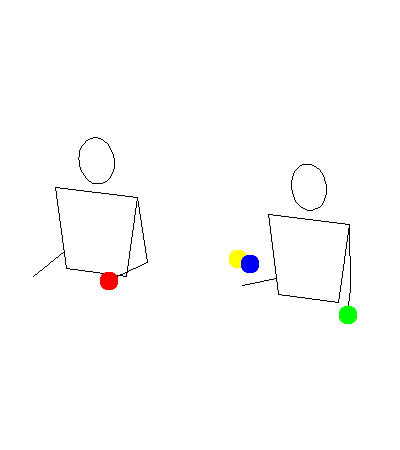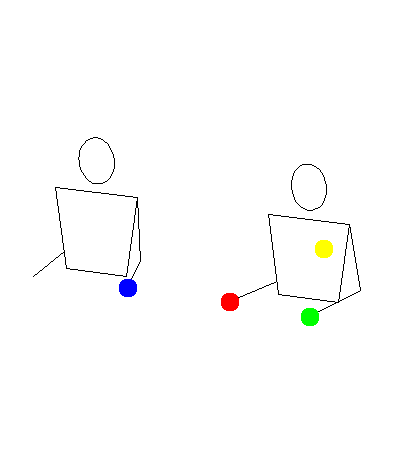
In a way, they are both right. My program was making it so a ball would land, then immediately get thrown. Michael’s idea was to have balls land as early as possible, then wait in the hand until it was time to throw again. This second way makes more sense for human jugglers because it gives lots of time to correct mistakes. I decided to add modes for both ways, and also a third mode at an interesting compromise point in between.

zero padding

I called my first implementation “zero padding”, since it fills empty time in the pattern with 0s.

two padding

I named Michael’s idea “two padding”, since it fills empty time in the pattern with 2s. I implemented it as an postprocessing step on top of my zero-padded translator.

Let’s go through an example by translating the siteswap 19 (5 ball shower) with hand order LMRM. The zero-padded translator says this should turn into <(2x,0)(0,ixp)(0,0)(0,ix)|(0,0)(0,0)(2xp,0)(0,0)> which looks like this:

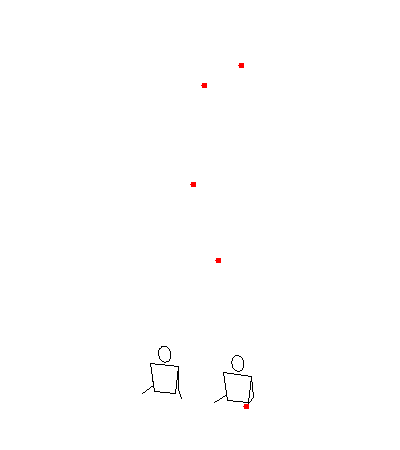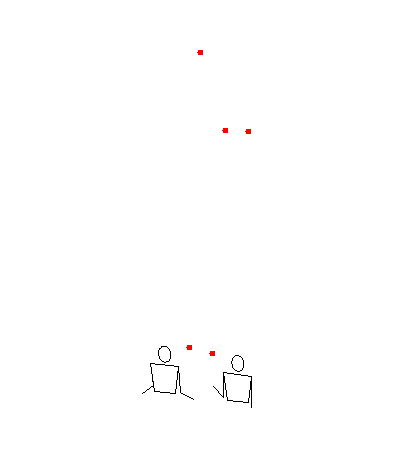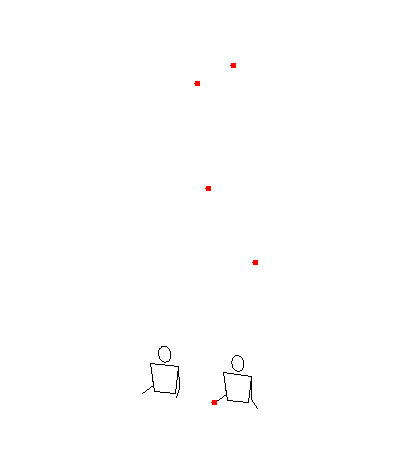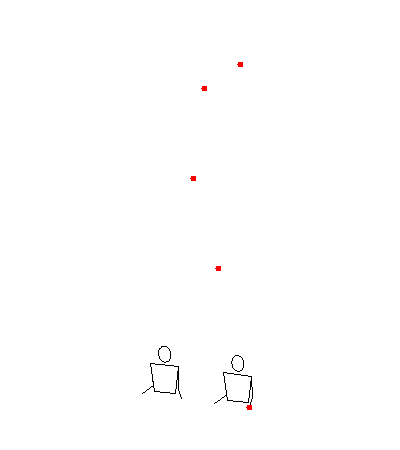
But let’s focus on the ixp throw. This throw goes up from the middle hand and lands in the right hand 9 beats later. And what is the right hand doing for those 9 beats?

1. 2x
2. 0
3. 0
4. 0
5. 2x
6. 0
7. 0
8. 0
9. catching our ixp and throwing a 2x

So this means we the ix is throw so high that the catching hand has to wait 3 whole beats of 0’s for it to land. Instead, let’s throw it 3 beats lower and replace those zeros with 2’s (holds). That results in <(2x,0)(0,cxp)(0,0)(0,ix)|(2,0)(2,0)(2xp,0)(2,0)> which looks like this:

The two sides of the pattern show exactly what the modification did. On the jugglers’ right, a balls is held for several beats before getting passed to the middle. On the jugglers’ left, a hand is empty for several beats before catching and immediately passing to the center.

We can also do this to the ix and end up with symmetric <(2x,0)(2,cxp)(2,0)(2,cx)|(2,0)(2,0)(2xp,0)(2,0)>.

light two padding

One thing that I found unsatisfying about two padding was that different 7’s in a siteswap might be thrown to different height. That’s because throws to the outside hands (in hand order LMRM) get lowered more than throws to the middle hand (which throws twice as frequently). As a result, siteswaps like 744 lost a lot of character. Here are some gifs of it rendered in both modes:

0 padded:

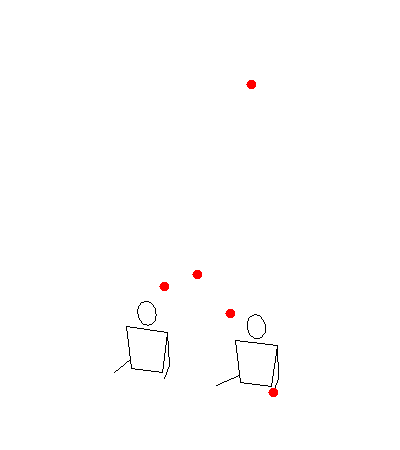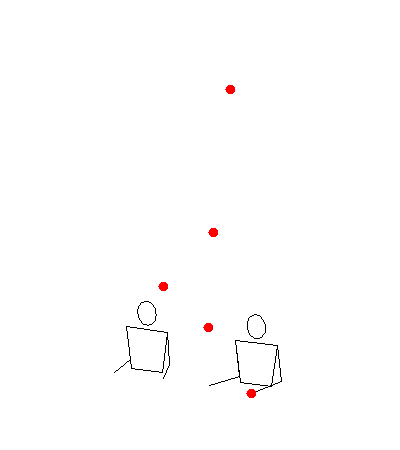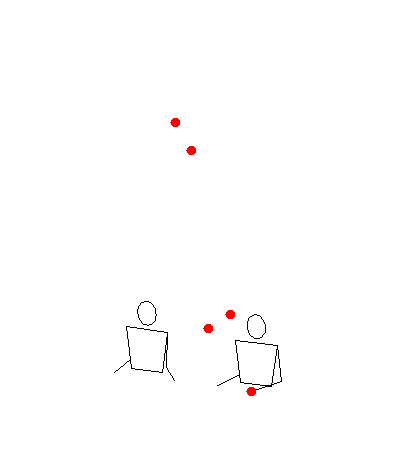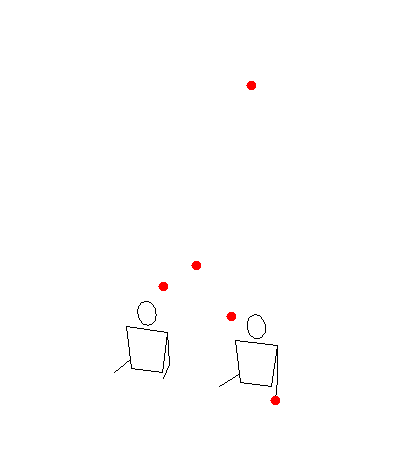
2 padded

To get around this, I added a version of 2 padding with a lighter touch, called “light two padding”. Rather than reducing all throws by the maximum amount, it reduces all throws by the same amount. This means relative heights are preserved and all 7’s go to the same height (which might or might not be 14). In this mode, 744 looks like this:

I think this mode finds a nice balance of preserving relative heights and avoiding unnecessary empty space. I’m really happy that Michael pushed back on my first implementation - the final program came out much better because of his input.

Multiplex Support

Once I had this working on vanilla siteswaps, a natural extension was to support multiplex siteswaps. The logic isn’t extremely different, but there is quite a bit of accounting to do when 2 padding a complicated multiplex siteswap. Here are some gifs to show what’s possible:

7b gattoplex in LMR:

7b gattoplex in LMRM:

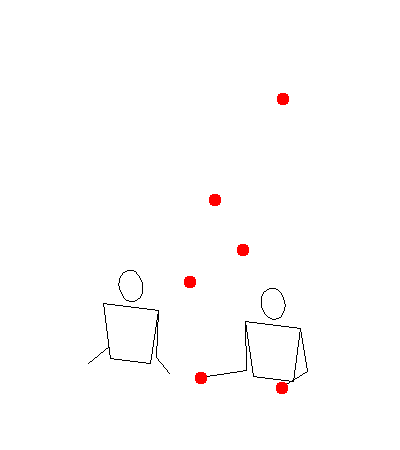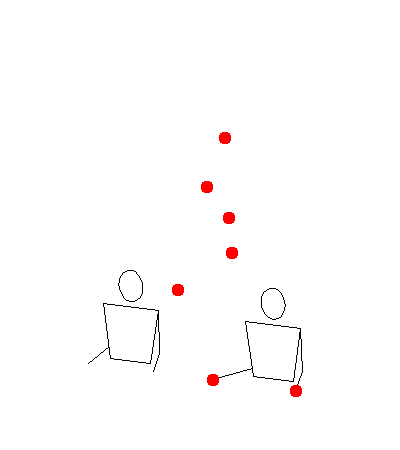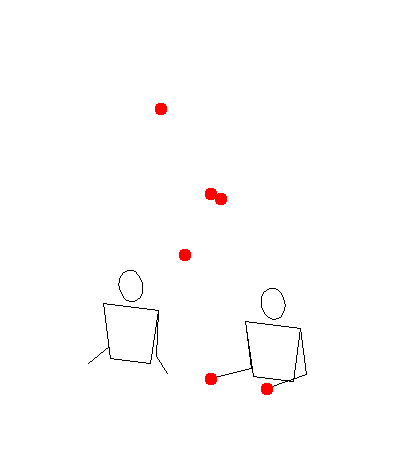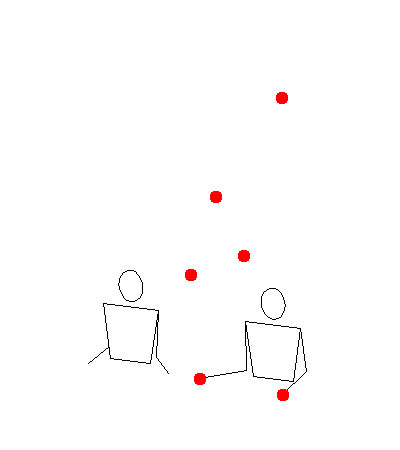
[345] with light two padding in llmmrr

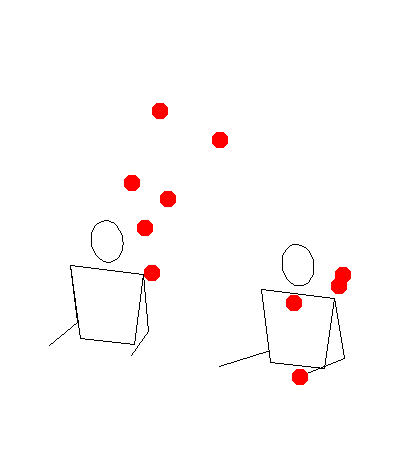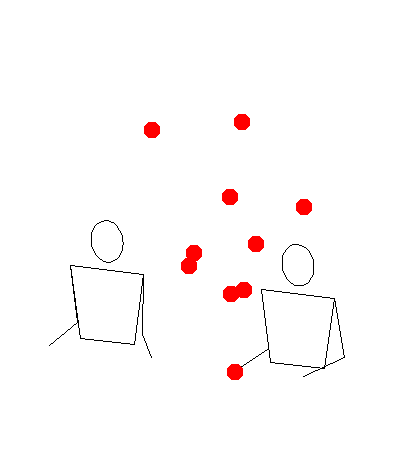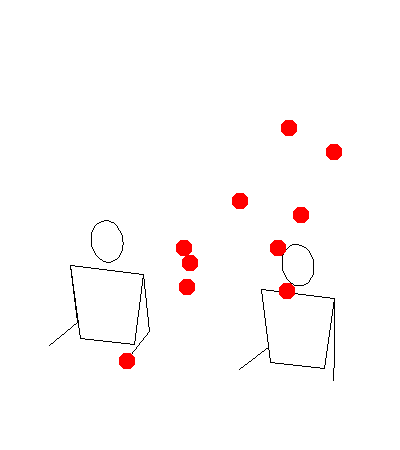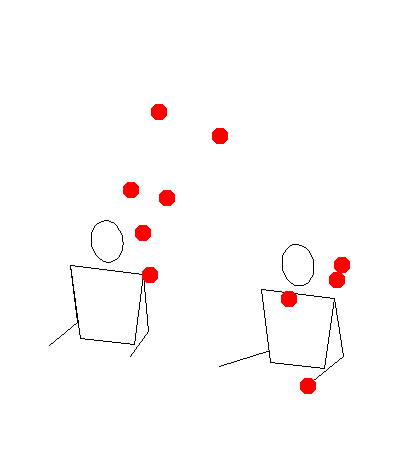
Remaining Work

I find that a lot of patterns look nicer (especially zero padded ones) when the bps in jugglinglab is increased. I still haven’t figured out how to determine the right bps though.

The Jugglinglab gif server times out after 30 seconds. That means complicated patterns, or ones with colors configured sometimes fail to render. You can work around this using the desktop or android apps but that’s not as convenient.

More Animations

I assume most people skimmed the math here and mostly looked at the pictures so here are some more animations for you:

368[56] in lmrm two-padded:

b97531 in llmmrr two-padded

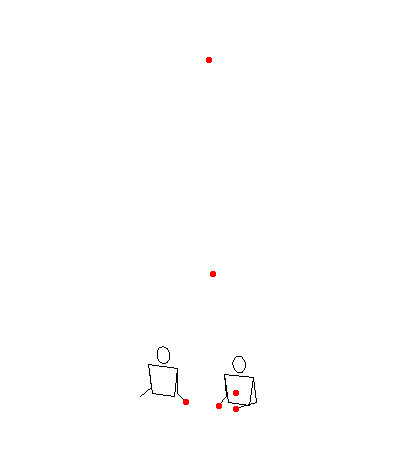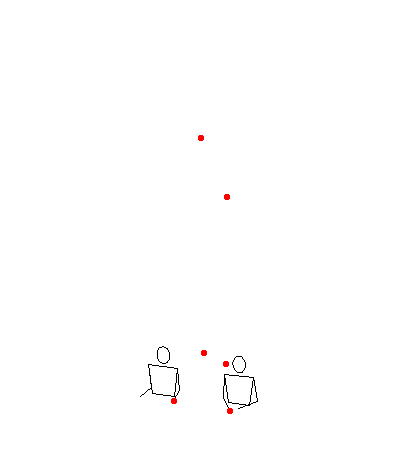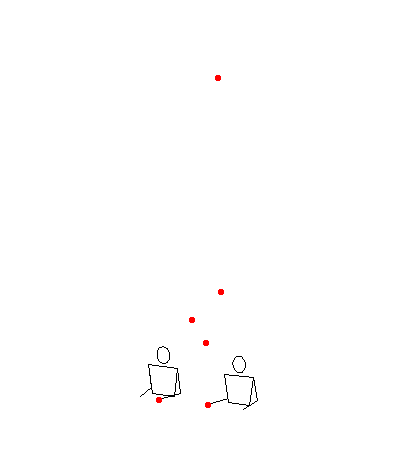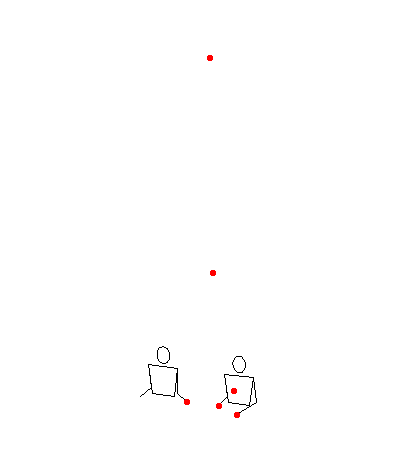
123456789 in lmrmrm with light 2 padding