tl;dr https://joshmermelstein.com/random-siteswap generates very random siteswaps. Read on to learn how it works.

Background

When James Buckland and I were working on juggling-graph, I sent him a worksheet from one of Matt Hall’s workshops to use for interesting examples. He turned that list into the “Random” button on that site. That button got me wondering - how would be generate siteswaps at random?

I did a bit of research and found a post from Jack Boyce, the author of jugglinglab. In it, he references this post from 1998 containing the following code:

/* gentest.c       Bijective siteswap generator        */
/*                                                     */
/* Jack Boyce (jbo...@physics.berkeley.edu)            */
/* July, 1998                                          */
/*                                                     */
/* Uses bijection to calculate all (b+1)^n siteswaps   */
/* of period n and no more than than b balls           */
/*                                                     */
/* Basic idea due to Colin Wright, Michael Kleber,     */
/* and many others                                     */

void convertone(int *in, int *out, int n) {
   int i, j, accum;
     
   for (i = 0; i < n; i++) {
      accum = out[i] = in[i];
      j = i;
      while (accum > 0) {
         j = (j+1) % n;
         if (in[j] < accum)
            out[i]++;
         else
            accum--;
      }
   }
}

void printthrow(int th) {
   printf("%c", th + ((th<10)?'0':('A'-10)));
}

void main(int argc, char **argv) {
   int i, bmax, n, *input, *output;

   if (argc != 3) {
      printf("Usage: gentest <ball limit> <period>\n");
      exit(0);
   }

   bmax = atoi(argv[1]);
   n = atoi(argv[2]);
   input = (int *)malloc(n * sizeof(int));
   output = (int *)malloc(n * sizeof(int));
   for (i = 0; i < n; i++)
      input[i] = 0;

   while (1) {
      convertone(input, output, n);
      for (i = 0; i < n; i++)    printthrow(input[i]);
      printf(" -> ");
      for (i = 0; i < n; i++)    printthrow(output[i]);
      printf("\n");

      i = n-1;
      while ((input[i] = (input[i]+1) % (bmax+1)) == 0)
         if (i-- == 0)
            return;
   }
}

His code works as expected, but I couldn’t figure out why it worked so I didn’t know how to extend it to support sync or multiplex patterns. Luckily, I did recognize the name “Michael Kleber” from the header comment - I know him through my work! Michael agreed to meet for coffee, and he gave me exactly the explanation I was looking for.

Cards Model of Vanilla Siteswap

First, we define a set of cards that look like this:

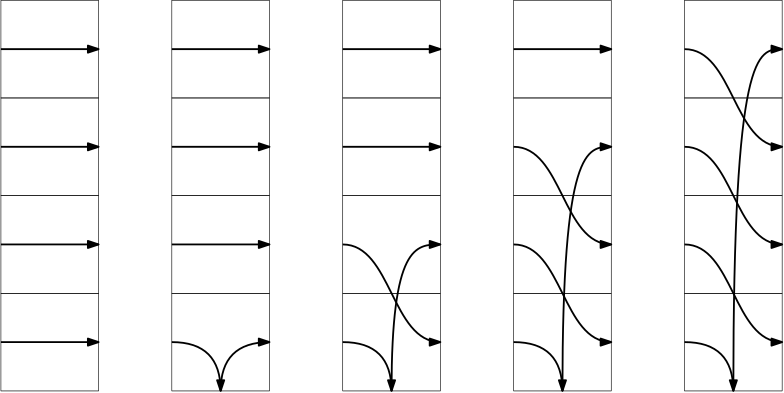
We’re going to generate our random siteswaps by drawing from a deck of these cards (with replacement). Here’s an example:

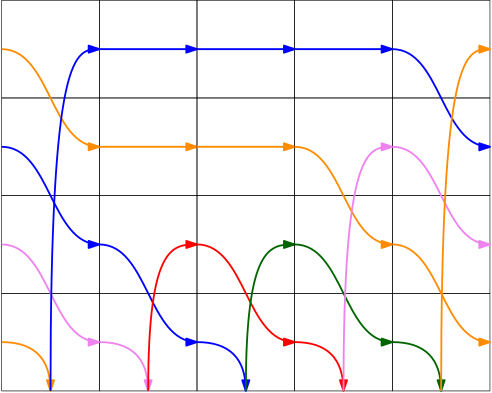
I’ve colored in various arrow to make things easier to follow. The first thing to notice is that every beat has one arrow “landing” on the bottom, and other arrow emerging from the bottom to some height. This is just like the conditions that make a siteswap valid.

The other thing to notice is that the cards divide space into evenly sized chunks. So we can count how many beats each arrow spends in the “air” before it lands back at the bottom of any card. If we do this for each arrow, we get the numbers {7, 2, 2, 3, 6}. And in fact, these cards can be viewed as a representation of the siteswap 72236.

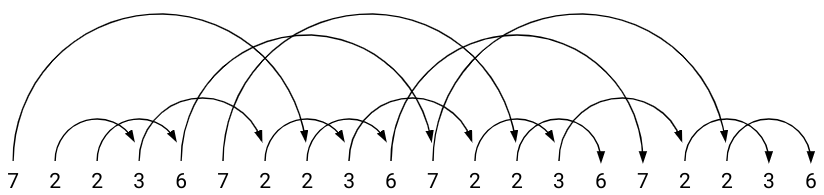
So why is this cards model useful to us? Well every arrangement of cards is a valid siteswap - and every siteswap has exactly one arrangement of cards. This simplifies the problem from “generating random siteswaps” to “generating random sequences of cards”. And we can represent each card with the height its arrow rises up to; so now we just need to generate a random list of positive integers.

Extending to Sync

Now that I understood the vanilla case, I wanted to extend this to generating sync siteswaps. The idea is really similar! Instead of our cards just having one arrow on them, they need two arrows - one for each hand. We could also use a pair of vanilla cards to represent each sync beat but we nee to be careful. If the second card was a 1, that would turn the first throw into a 0x. Here’s an example of a hand of sync cards.

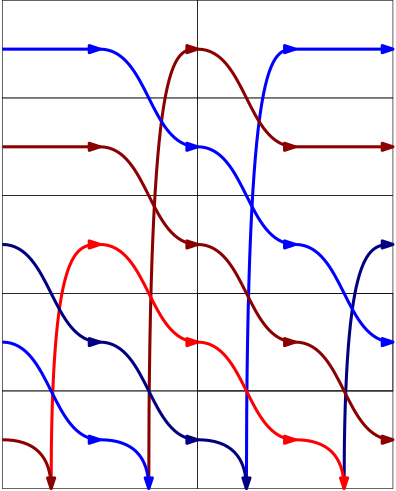
Can you tell what siteswap this is? Check the name of the image for help.

Extending to Multiplexes

Extending to multiplex is also not too difficult. Now, we allow more than one arrow to rise from the bottom of each card, and we also make sure that the same number of arrow go to the bottom of each card. For example, here are all cards of height 3 (ignoring the order that balls exit a multiplex).

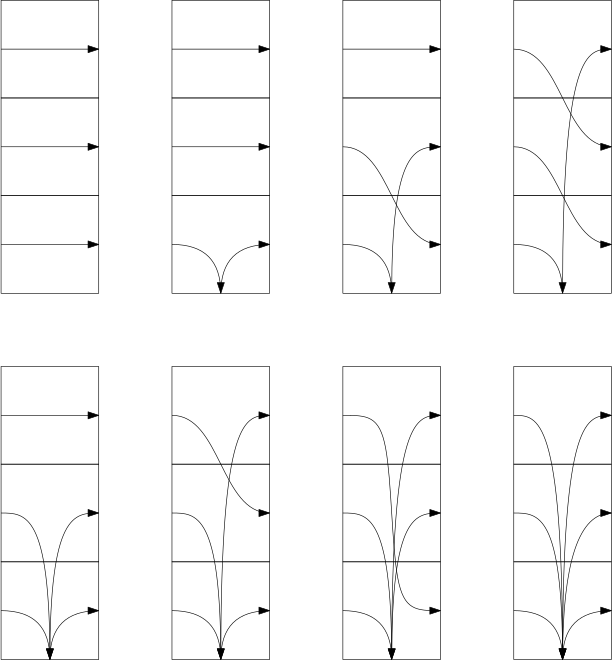
Now that more than one arrow can hit the ground in a card, we need to modify our constraint on sync card pairs. The new constraint is the “the lowest height on the first half of a card must be higher than the number of arrows coming out of the second card. As before, this guarantees that no 0x’s will appear.

Problems with multiplicity

Of the 8 multiplex cards shown above, there are 4 from the vanilla deck, and 4 new ones - so if we pick randomly then we have a 50/50 shot of introducing a multiplex. But what happens as the max arrow height goes up?

Well when there are n heights to choose from, there are 2^n possible cards, and only n+1 are vanilla. When N is large, that’s a tiny fraction!

So if we generate cards uniformly at random, we’ll end up with nearly every throw being a multiplex. There’s nothing wrong with this but I think those patterns aren’t that interesting. I decided to make high multiplicity throws much less likely to steer the program toward patterns I found interesting.