Using Bandaged Cube Explorer to solve 0x20108000000C03
Background
In my previous post, I introduced a tool for exploring the shape space of bandaged 3x3x3 Rubik’s cubes and suggested that it might be useful for solvers. In this post, I’m going to walk through how I how I used it to solve one bandaged configuration, 0x20108000000C03.
I decided to name this puzzle “cofortress” since its shape graph has the same structure as the one for Bandaged Fortress (a.k.a. 0x30000010048883)

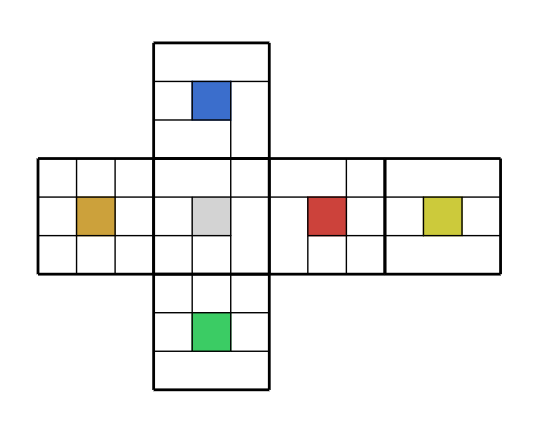
Analyzing the cube
For consistent naming, I assume that the cube is always oriented with white on the U face and green on the F face.
Cofortress has a small state space, just 42 nodes and 60 edges arranged in one big loop. As you walk around the loop, there is a repeated pattern - “half turn, half turn, quarter turn (solver picks direction)”. This suggests that our sequences will have one of two forms:
- Go around the loop
- Go partially around the loop, until you hit a quarter turn. Do that quarter turn twice to swap some pieces, then undo the path around the loop.
There are arguably others where we take a more complex back-and-forth path around the loop but all of these can be written as combinations of the above so I don’t really consider them.
If we look closely at the states where a quarter turn is possible, we notice that they always happen on a face with with two 1x1x3 blocks and two regular edges. This means our second type of sequence should always swap two edges and swap the 1x1x3 blocks.
By the same reasoning, following the whole loop will have the same effect on the other bandaged blocks and the unbandaged corners no matter which direction we choose to take our quarter turns. It happens to be the case that this effect is nothing; so when cofortress is solved by shape, our 1x1x2 blocks and unbandaged corners are always solved by color.
What is left for us to solve are the 9 pieces on cofortress that can move around when the puzzle is solved by shape:
- The two 1x1x3 blocks can swap with each other
- The {UF, UL, BL, FL, FR, DL, DR} edges
But wait - when cofortress is solved by shape, a D2 move swaps the 1x1x3 blocks. So now we’re down to two remaining challenges; getting to the solved shape, and finding ways to move unbandaged edges around in the solved shape.
Solving the shape (and scrambling the puzzle)
This might sound surpassing if you’ve never held a bandaged puzzle but scrambling them can be a challenge in its own right. On cofortress, the turns out to be almost the same challenge as solving the shape.
Looking closely at our shape graph, each state has either one or two faces that can turn. That means that we can walk the loop (without needing to see it) by always turning a different face than the one we turned previously. Even better, we use the “half turn, half turn, quarter turn” pattern to guide us. The first half turn will always effect just one of the 1x1x3 blocks. The second half turn will effect the other, then the quarter turn will be on the face that now contains both of them.
I case you’d like something a big less handwavey, here’s a sequence to follow for scrambling cofortress:
B2 U2 F*
L2 B2 R*
D2 R2 D*
B2 D2 B*
R2 F2 L*
U2 R2 D*
Where * means either a clockwise or counterclockwise quarter turn. I’ve found that even one repeat of this sequence is a decent scramble but feel free to go through it a few times.
When it comes to returning cofortress to its solved shape, the procedure is similar to the scramble. Put both 1x1x3 blocks on the same face, then follow the “half turn, half turn, quarter turn” sequence until both are solved relative to the centers.
Edge Orientation
People who haven’t spent much time with a Rubik’s cube sometimes think that it is a puzzle about manipulating 54 independent stickers. In fact, that puzzle is made of a core, eight corners and twelve edges. Ignoring the core for a moment, the corners and edges both have a position and an orientation on the cube. Its possible to put all pieces in the correct position, but have some 3-sticker corners twisted or some 2-sticker edges flipped in place.

On cofortress, the constraints imposed by the bandaging mean that when we are in solved shape, or corners are always oriented correctly. In the first draft of this solution, that made me overlook the fact cofortress can still have flipped edges. Rather than walk you through my faulty thinking, let’s discuss what it means for an edge to be oriented and then skip ahead to when I corrected myself.
Speedcubing methods provide a nice definition for edge orientation. We consider an edge oriented if it can be put into place (on an unbandaged Rubik’s cube) without using the F and B turns (or the slice turns). If you don’t have a lot of experience solving a Rubik’s cube, the speedcubing definition can be hard to visualize so here’s a equivalent procedure that spells things out more explicitly.
# Assume the cube is oriented with white on top and green in front
# If using a different color scheme or orientation, relabel colors accordingly
if edge is on the U or D face:
let C1 be the color of the sticker on the U/D face
let C2 be the color of the other sticker on that edge
else:
let C1 be the color of the sticker on the F/B face
let C2 be the color of the other sticker on that edge
if C1 is white or yellow:
the edge is oriented correctly
if C1 is orange or red:
the edge is flipped
if (C1 is green or blue) and (C2 is red or orange):
the edge is oriented correctly
if (C1 is green or blue) and (C2 is white or yellow):
the edge is flipped
Edge orientation is a broadly useful concept for all kinds of solvers.
- The ZZ method starts solve by orienting all edges - then takes advantage of this invariant in later steps.
- Competitors in the Fewest Moves Challenge event in the World Cubing Association have a number of techniques for finding efficient solutions to a scramble. One popular technique is Domino Reduction, which uses edge orientation for a similar reason - this invariant can be taken advantage of later in the solve.
In the case of our bandaged puzzle, we care about edge orientation because we have a lot less flexibility with edge orientation than with edge permutation so our plan is to orient all edges before permuting them.
Moving Edge Around
With our analysis out of the way, let’s start to look at some concrete sequences
on cofortress. We’ll begin with those of the second type mentioned above,
conjugates setting up to a half turn. We know that these will swap the two 1x1x3
blocks and two unbandaged edges so let’s apply them to a cube and see which
edges are swapped. To keep these compact, I’m using the twisty puzzles shorthand
for conjugates, [A : B] = A B A^-1 where A and B are arbitrary sequences.
Here are 9 sequences that swap the two 1x1x3 blocks and also swap a pair of edges without modifying their orientation.
| id | sequence | edges swapped |
|---|---|---|
| perm 1 | D2 | DL, DR |
| perm 2 | [B2 U2 : F2] | FL, FR |
| perm 3 | [D R2 U2 : L2] | FL, BL |
| perm 4 | [B2 U2 F L2 B2 : R2] | UL, DR |
| perm 5 | [D R2 U2 L F2 R2: B2] | UF, DR |
| perm 6 | [D R2 U2 L F2 R2 B D2 B2 : D2] | UL, FL |
| perm 7 | [D R2 U2 L' F2 R2 B D2 B2 : D2] | UL, BL |
| perm 8 | [D R2 U2 L F2 R2 B D2 B2 D R2 D2 R B2 L2: F2] | FL, DR |
| perm 9 | [D R2 U2 L F2 R2 B D2 B2 D' R2 D2 R B2 L2: F2] | UL, DL |
Next we have 3 sequences that swap the two 1x1x3 blocks and also swap a pair of edges and also modify the orientation of both swapped edges.
| id | sequence | edges swapped |
|---|---|---|
| flip 1 | [B2 U2 F L2 B2 R D2 R2 : D2] | UF, FR |
| flip 2 | [B2 U2 F' L2 B2 R D2 R2 : D2] | UF, FL |
| flip 3 | [D R2 U2 L' F2 R2 B D2 B2 D R2 D2 R B2 L2: F2] | DL, BL |
And now let’s talk about sequences of the first type, where we make a circuit around almost the whole shape space of cofortress. I found these did a lot more than the type-2 algorithms above so they weren’t as useful for moving just a few edges. Some of them were nice for flipping more than two edges at a time, but this is an optional optimization.
| id | sequence | edge slots flipped |
|---|---|---|
| circuit 1 | D R2 U2 L F2 R2 B D2 B2 D R2 D2 R B2 L2 F U2 B2 | UF, FL, DL, DR |
| circuit 2 | D R2 U2 L' F2 R2 B' D2 B2 D R2 D2 R B2 L2 F U2 B2 | UF, BL, DL, DR |
| circuit 3 | D R2 U2 L F2 R2 B D2 B2 D' R2 D2 R B2 L2 F U2 B2 | UF, UL, DL, DR |
Careful readers might have noticed that some of these sequences differ only by the direction of a quarter turn (i.e. perm 6 vs perm 7). But there are some variations of these algorithms that aren’t listed above. The sequences that I omitted are because they have the same effect as a sequence in the table. For example, replacing the D in sequence 3 with a D’ doesn’t change which pieces are swapped so including it would be redundant.
Using the Sequences
Like with edge flipping, our options for which slots can be swapped are somewhat limited. Some slots are easier to use than others. In particular, the UF slot is annoying to insert into but is critical for all flipping sequences. Here is a visualization of which slots can swap with which others without changing edge orientation.
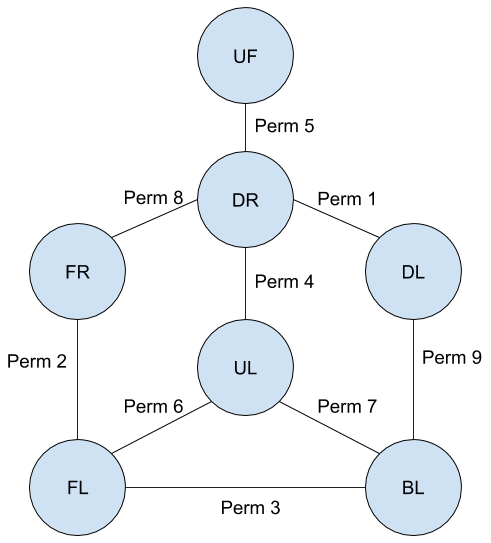
So to bring it all together, we use the visualization and perm sequences above to set up flipped edges into positions where they are easy to orient correctly. We use the flip and cycle sequences to orient them. Finally we use the visualization and tables again to move the edges back to their solved slots.
It’s worth noting that all our perm algorithms are conjugates so their ends are the inverse of their beginnings. This means they can cancel quite a few moves when doing one after another. For example, consider perm 5 followed by perm 3:
[D R2 U2 L F2 R2: B2] [D R2 U2 : L2]
(D R2 U2 L F2 R2 B2 R2 F2 L' U2 R2 D') (D R2 U2 L2 U2 R D')
D R2 U2 L F2 R2 B2 R2 F2 (L' U2 R2 D' D R2 U2 L2) U2 R D'
D R2 U2 L F2 R2 B2 R2 F2 L U2 R D'
This is exactly the same as perm 5 except with the last L’ replace by an L. So if you know the next several sequences you are going to do, you can optionally save moves and time by predicting which moves will cancel and omitting them.
Final Thoughts on Cofortress
I quite enjoyed solving cofortress. Now that I have my method and notes organized, it only takes a few minutes to scramble and solve it. I really like how different the solve feels from an unbandaged 3x3x3.
I’m also happy with how my bandaged-cube-explorer tool guided my solve. It certainly would have been possible without the tool but I think it would’ve added a lot of toil with adding much enjoyment.
Bandaged Fortress
A small update - since writing this post I spent an evening analyzing and solving bandaged fortress. As expected, the solve feels very similar to cofortress. My solve’s outline looks the same - follow “half turn, half turn, quarter turn” until the puzzle is solved by shape, orient all edges, then permute all edges.
When I feel like coming back to this sort of bandaged puzzle, I think I may try one of 0x20100000000C03 or 0x30000000040203 next. The first one severs one of the bonds in cofortress resulting in a graph with a second loop. The latter one takes it a step further and moves a block to allow for 4x as many states as cofortress, arranged into 4 connected loops.